Nyquist Sampling

In the early 20th Century, during the dawn of digital electronics, Harry Nyquist (and various others) realised that to accurately represent a continuous (or analogue) series in a discrete (or digital) way would require that the representation, or recording, of the continuous series be at least twice its frequency. An everyday example of this phenomenon is the the recording of audio into digital formats at a frequency of at least 40 kHz (typically 44.1 kHz or greater is used). This is because the human auditory system (an analogue recording device) is generally capable of detecting frequencies up to 20 kHz. If the audio was recorded at less than 40 kHz, the high frequency treble sounds would be lost. The lower the recording frequency, the worse it would sound.
We can represent this as follows:

The red line is the continuous series we wish to record as a digital signal. The black dots are the frequency at which we record. The dashed line is thus the digital representation of the signal. It is obviously different than the original series!

A visual example of this is the moiré pattern seen in images that are resized or captured at low resolution:

In the case of imaging in three dimensions on a fluorescence microscope, we therefore need to set our image size (or more technically, our pixel size) and our step size (Z) appropriately.
The well-known Abbe equation tells us the limit of lateral (XY) resolution:

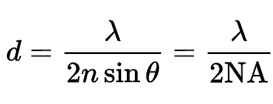
For example, using 525 nm light and a high NA objective, such as a 1.4 oil, this is 188 nm.
Nyquist sampling theorem tells us that our digital sampling should be at least twice this frequency (or half the distance), or that our pixel size (in the image plane) should therefore be no larger than 94 nm.

If we are using a total magnification (C-mount and objective) of 100x, this equates to a 9.4 μm pixel on the camera.

The following formula tells us the limit of axial (Z) resolution:

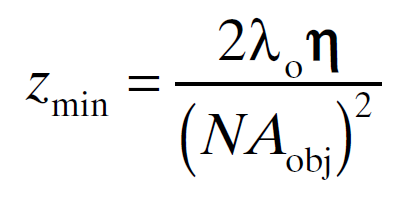
Where η is the refractive index of the medium.
Using the same example as before and 1.518 as the refractive index, this is 813 nm. Nyquist sampling theorem tells us that our Z-step size should therefore be no larger than 406.5 nm, or 0.4 μm.

The take-home message is this: The more information that can be provided to the deconvolution processing, the better the resolution and SNR in the final image.

Within the usual restrictions of imaging with samples that may be sensitive to bleaching and/or phototoxicity, the smallest pixel size and smallest Z-step practical should be used.